Sheaf theory for data science

For my PhD dissertation, I worked on applications of topology to data science. I used cosheaves and spectral sequences to compute persistence in a distributed manner. I applied such distributed computation to study multi-density data and recovered the information lost in persistence diagrams.

For example, consider the following point cloud and its coresponding persistence diagram in dimension one.

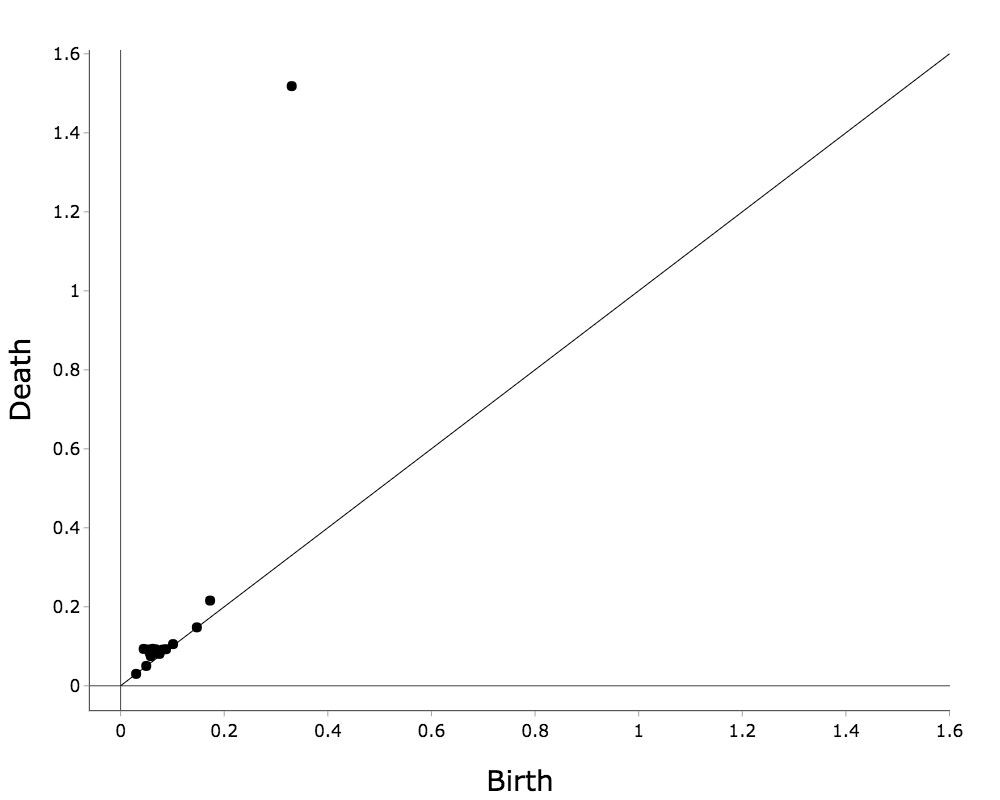
By observing the persistence diagram, one would conclude that there is one significant feature. However, one can see from the point cloud that there are small but significant features that are densely sampled. My construction of distributed computation allows one to identify such significant features that are neglected by traditional methods.

Here is a 30 minute video of my presentation at IMA special workshop on Bridging Statistics and Sheaves.

The paper can be found on arXiv. Here is a copy of my PhD dissertation.

University of Pennsylvania (2013-2018), PhD dissertation. Joint work with Robert Ghrist (U. Penn).